Newsletter of the Bachelier Finance Society

Volume 11, Number 2, April 2019

JOB POSTINGS

The aim of these postings is to create a forum for the dissemination of information on academic and industrial positions related to mathematical finance, across different disciplines and different geographical regions. Please submit any job advertisements you are aware of to jobads@bachelierfinance.org, preferably in plain text and sending the link to the website containing all the information. Updates and new items appear continuously at: http://www.bachelierfinance.org/forum/jobs/.

The Society maintains a list of books, book reviews and journals at: http://www.bachelierfinance.org/publications.html. Members that would like to have their books added to the website, should please let us know.

Recently published books

Mark H. A. Davis
Mathematical Finance: A Very Short Introduction
Oxford University Press (2019), ISBN 9780198787945

INTERVIEW WITH UWE WYSTUP

Could you explain what makes FX options special compared to e.g. equity options or other assets classes?

FX options started as hedging instruments for corporate treasurers, and are therefore bespoke, traded over the counter, and help internationally active companies survive. Equity options are traditionally investment vehicles nice to have for speculators, but not actually needed. The market is much less liquid and often uses standardized listed options, which in FX has just started. The academics used to favor equity options for a long time and all worked on the same S&P500 data set, as it was publically available. And derivatives were first systematically taught in the US, where FX isn’t on anybody’s radar, because we’ve already got the US dollar. Consequently, an entire generation of students thinks that options are equity options and some of them have now become professors. But to keep in mind: it is the FX options that have always been the more liquid, more commoditized and advanced in models. In terms of pricing options, it all starts with market data, its quality, availability and conventions. Nowadays, both currency and equity options quants need to construct a volatility surface, i.e. a function returning the Black-Scholes implied volatility for a given strike and maturity. The input in FX often comes in terms of implied volatilities on the delta space for at-the-money options and structures like butterflies, strangles and risk reversals, along with several conventions; we typically have 3-5 observation points. The input in equity options markets typically comes directly in the form of implied volatilities for a set of strikes, but contains many more strikes. Therefore, for equity options, the volatility smile is often constructed using non-parametric statistical approaches, whereas in FX options, there are still popular parametric curves like SVI and polynomials.

You mention in the Preface of your book “FX Options and Structured Products” that “the key to really understanding options is the foreign exchange market”. Could you elaborate on this? 

Only in FX can you see the symmetries, and suddenly everything starts making sense. To give you an example, the value of a call option in the Black-Scholes model can be calculated using the Black-Scholes formula: S N(d₊) – K N(d_–). I am dropping the discount factor(s) here for simplicity. When I was a student, I learned that the first probability N(d₊) is the delta of the call option, i.e. the number of the underlying units a trader needs to buy to delta hedge – or the investment amount over time for the self-financing strategy, the academics would phrase it. For a long time I asked myself, why is this delta given by N(d₊), and not by N(d_–)? Shouldn’t there be a quota? I just never found this quite fair, let alone mathematically clear. FX can teach us the answer: N(d₊) is the delta if the premium of the option is paid in USD, and N(d_–) is the delta if the premium is paid in GBP, assuming the underlying is cable, i.e. the price of a British Pound (GBP) in US Dollars (USD). Sometimes, things are as simple as that. Both probabilities have the delta-interpretation and both are correct, and both reflect daily trading practice. The notation using + and – rather than 1 and 2 reflects my view on this: options are symmetric.

What are the main changes in FX markets in the 10 years since the publication of the first edition of your book?

1. The successful market makers, and there about 10 of them globally, are now trading FX options like commodity products on their electronic trading platforms. Spreads have come down, regulation is often anti-business oriented and interpreted in a way to better shut down derivatives and structured products business, consequently liquidity has decreased. But the platforms have become really good and professional.
2. The rather crazy product innovation cycle of the 90s and early 2000s has ended, and been replaced by payoff-language based valuation.
3. The sell-side has upgraded volatility surface construction from spreadsheet functions to robust fitting engines, and the pricing models for exotics from vanna-volga to stochastic-local volatility models or mixed local volatility models, for emerging markets, sometimes even with jumps.
4. Independent pricing platforms have smaller fan clubs (SuperDerivatives sold, Reuters Eikon rebuilt), as you often get tradable prices on single-dealer platforms.
5. Central banks and geopolitics are more influential in the FX spot market.
6. The Chinese Yuan and its options market is growing like never before.

What are the main new features in the second edition of your book?

It is basically a new book. Many of the quantitative topics have been moved to a second volume, which I am working on, but the current second edition is a book on products and markets. Hence, the key innovation of the market in first decade has been added as an entire chapter: Target Forwards. These have become flow products now and are even traded on electronic platforms. A Target Forward is an agreement to buy GBP and sell USD every week at a price higher than the market outright forward rate, and yet trades at zero cost for the buy-side. The catch is that, since the buyer is likely to make a profit every week, all remaining weekly cash-flows will be cancelled once the accumulated profits reach a pre-specified target. Both the seller and the buyer will then be happy and trade the next target forward. You can imagine that this is a hot bun. Other updates in the book include new accounting rules, applied to FX structured products, and a separate solution manual for dozens of exercises.

There are a lot of special greeks mentioned in the book: speed, charm, color, volga, vanna, … What do they express and how are they used by practitioners? 

Yes, the Greeks are funny. Well, generally, the Greeks tell the trader the answer to the “what-if?-question”, e.g. what happens to my portfolio if the spot moves down and at the same time volatilities rise? A trader always needs to be prepared for changing markets, and does consider these effects to higher orders. As mathematicians, we are probably easy to convince that an approximation using a Taylor-series shouldn’t always stop at the linear term. A trader uses ratios of Greeks for hedging, e.g. if vanna of an exotic option is 20, and vanna of the liquid instrument he can trade (the risk reversal in this example) is 10, then he would buy 20/10=2 risk reversals. Risk-managers and controllers in sell-side institutions run daily Delta-Gamma-Vega reports, so they need the Greeks too, but here first order is sufficient. Finally I am getting myself amused by terms like vanunga, volunga, bufga and refga, and thought I might as well share this with the community.

Could you give some examples of structured products and exotic options that are useful to corporate treasury? 

Very simple: the county of Rheingau-Taunus (near Frankfurt in Germany) had lost about 80 Million EUR from taking their loans in Swiss Francs (CHF) rather than Euros (EUR). The loss had become astronomical on 15 January 2015, when the Swiss National Bank (SNB) stopped protecting the 1.2000 level and spot had dropped to levels even below 1.0000, but then slowly recovered, see Figure 1.

Figure 1: EUR-CHF drop and recovery in 2015

Political pressure forced the county to materialize their book loss. In the exit strategy a standard FX forward was used. A structured FX forward like a shark forward could have saved the county EUR 2 Million, had it been applied. The book contains a chapter of case studies just around these questions and covers exit strategies of sick floans (foreign currency loans).

What are the most useful (least useful) options or products on the market for investors?

Investors? Or Treasurers? This makes the critical difference, as the client type treasurer has the underlying cash-flow, for which he needs a hedge, whereas the client type investor doesn’t. Consequently, zero-cost structures are dangerous for investors, but for the danger to come, even a simple forward contract is already sufficient. Risk doesn’t necessarily rise with complexity. Which product is useful really depends on the given circumstances. And as mathematicians, we would probably first want to define the term “useful”. It is easier to talk about how popular products are. For instance, ISDA has standardized deal confirmations for FX variance and volatility swaps in 2013, which clearly shows a huge appetite from institutional investors.

What options are the easiest (hardest) to hedge / manage? 

Easiest: power call on USD/JPY, as there are no kinks in the payoff, no nasty gamma peaks, hardly any slippage. Slippage means that the market moves faster than you can react in your hedge. So it becomes easy if Greeks are small and stable and the underlying is super-liquid.

Hardest: products with jumps in the payoff, like even a simple European digital with one day left to expiry. Or anything with an incomplete market, i.e. hedging instruments are not available or very illiquid or very expensive. In FX this would be vega of illiquid crosses (e.g. Turkish Lira against Brazilian Real) or anything long-term.

You mention that the Black-Scholes model is inappropriate for exchange rate modeling. Could you explain why this is so and what more appropriate models are? 

The Black-Scholes model assumes that FX spot returns are normally distributed. It is well-known that they are not, as they typically are leptokurtic: i.e. more mass in the center and in the tails, less between. However, the Black-Scholes model is used by all practitioners to price vanilla options, because all that happens is that you plug the volatility into the Black-Scholes formula. The modeling has been moved to volatility surface construction. So it is definitely important to teach students the Black-Scholes model (also so they can do some exercises). For smile surface construction, one considers various inter- and extrapolation methods illustrated in Figure 2. For example cubic splines often overfit and can lead to negative probability densities. The more popular SVI (stochastic-volatility-inspired) parametric fit must be applied with care to prevent too kinky curves (extreme case of a conic section). 

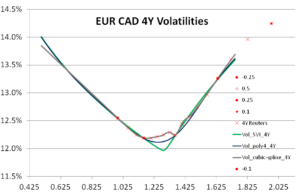
Figure 2: EUR-CAD implied volatilities on the strike space with interpolation

In most cases, the market data is the problem rather than the model. For path-dependent derivatives, one tries to capture the spot and volatility dynamics by mixing stochastic and local volatility models.

What about jump risk? Is this an issue in FX modeling? 

Jump risk typically prevails in pegged-currency pairs such as USD-HKD (Dollar-Honky), SAR (Saudi Arabian Riyals), or even temporarily for EUR-CHF. The SNB action mentioned above made it extremely clear to a wide audience of affected market participants that this is actually a huge risk. In modeling, volatility surface construction can take into account the market prices of variance swaps, which contains the information of how the market gauges the jump risk. Jump-diffusion models are used in practice too, and are available on commercial pricing platforms. Ernst Eberlein and his fan club must be jumping of joy.

What about model risk? Is this measured? And if so, how? 

Measuring model risk is a standard requirement of Model Governance. You can’t submit an application for the introduction of a new derivative to the regulators anymore without a detailed analysis of the model risk involved in pricing and risk managing this derivative. For example, consider a simple double-no-touch (DNT) contract, which pays a fixed amount of currency at maturity if the spot remains inside a pre-specified range between inception and expiry. The models one considers here include Black-Scholes (for what traders call the theoretical value (TV)), vanna-volga, local volatility, at least one stochastic volatility model (e.g. Heston) and a mixture model. Prices of various models for exotics are often visualized in so-called mustache graphs with TV on the x-axis and the difference of a model price and TV on the y-axis. In Figure 3 we observe that a local volatility model underprices the DNT, whereas the Heston model overprices the DNT. 

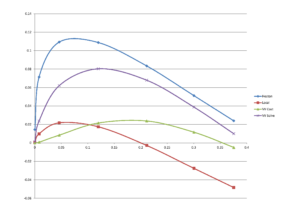
Figure 3: Difference to Theoretical Value of Four Pricing Models for a 6-month Double-No-Touch in EUR-USD

Additional features one considers include hedge performance of the model-derived Greeks, stability of Greeks and spot-vol-ladders, stability of calibration and the resulting model parameters, complexity, computation time, suitability for bank-portfolio risk analysis.

With Brexit looming: What could investors do to protect their EUR-GBP exposure (think e.g. of someone who lives in the Eurozone, but still has a bank account in the UK)? 

GBP volatilities have been surprisingly low for a while now, both against EUR and USD. I guess the market has stopped taking this political show in the UK seriously. The book doesn’t say anything about FX spot rate forecasting, as I personally don’t believe in it. After a move in the spot you will always find someone who will say that he has always predicted this. So whether you want to sell your pounds or hold on to them, I am sorry, I can’t help you with that. For the corporate treasurer, the wide range of FX structured forwards would do a good job. There is something that works for both importers and exporters, and for low volatilities and high volatilities, and for highly skewed volatility curves as well as almost flat curves. For instance, at 24 January 2019’s market data, an exporter in the US who needs to sell Sterling in 6 months can lock in a guaranteed worst case equal to current spot 1.3000 USD per GBP, but participate in GBP rising up to a level of 1.4000, should the spot stay below this level. This FX structured forward has zero cost for the treasurer and contains a reasonable profit for the sell side. If GBP drops, the 1.3000 worst case is guaranteed. This is very easy to sell. In EUR-GBP, the GBP buyer/EUR seller could currently lock in a similar zero-cost structure with worst case of 0.8700 equal to the current spot and participate in a weaker GBP up to a level of 0.9300, i.e. get 6 big figures participation for free.

What is your opinion on crypto currencies? Are they going to affect FX markets in the future? 

In my opinion, crypto currencies are the only real innovation in financial products in the last 10 years, and many of them will continue to play a major role in financial markets. In fact, crypto currency derivatives are beginning to trade, even options.

To what extent are crypto currencies just another set of currencies? What is different or special about crypto currencies when compared to standard currencies? 

Crypto currencies can be considered cash or a commodity rather than a standard currency, as they are not backed by central banks and don’t pay any interest, but one rather has storage cost and risk of theft. Implied volatilities tend to be bigger by a factor 10, e.g. 80% for bitcoin compared to 8% for EUR/USD. Smiles are not as skewed as they can be for standard currency pairs, and one can still spot violation of put-call-parity in crypto currency implied volatilities. The crypto derivatives market is in its very early stages, whereas the standard currency derivative market is highly advanced.

How do technological advances (machine learning, data science, artificial intelligence, etc) affect FX markets?

FX markets have been discovered by institutional investors a while ago, and obviously there are investment strategies created by machine learning algorithms trying to increase performance. For the technology part, we see advances in model calibration using machine learning. However, for the moment there is first of all a big hype about it: with these key words it is easier to appear innovative and get budgets approved.

The interview was conducted by Natalie Packham (HWR Berlin) and Antonis Papapantoleon (NTU Athens).

UPCOMING CONFERENCES

This list contains conferences related to mathematical finance that take place in the next three months. A full list is available at http://www.bachelierfinance.org/congresses/conferences.html. Please let us know of conferences we are not aware of and include a URL for the event.

Mean-field games, energy systems, and other applications
April 1–5, 2019
Edinburgh, UK

MathFinance Conference
April 8–9, 2019
Frankfurt, Germany

2nd Leeds Conference on “Stochastic Control and Games Under Ambiguity”
April 8–9, 2019
Leeds, UK

Workshop on Frontier Areas in Financial Analytics
April 29 – May 3, 2019
Toronto, Canada

QFin@Work2019
May 3, 2019
Rome, Italy

stresstest2019 : International Workshop on Stress Test and Risk Management
May 28–29, 2019
Paris, France

New Frontiers in Stochastics for Economics and Finance
May 30 – June 1, 2019
Siena, Italy

SIAM Conference on Financial Mathematics & Engineering (FM19)
June 4–7, 2019
Toronto, Canada

Rutgers Equilibrium Theory Summer School & Workshop
June 10–13, 2019
New Brunswick NJ, USA

9th General AMaMeF Conference
June 11–14, 2019
Paris, France

Insurance Data Science Conference 2019
June 14, 2019
Zurich, Switzerland

3rd ICASQF (International Congress on Actuarial Science and Quantitative Finance)
June 19–22, 2019
Manizales, Colombia

International Conference on Financial and Energy Markets: Modeling and Simulation
June 20–22, 2019
Cagliari, Italy

Commodity and Energy Markets Association (CEMA 2019)
June 21–22, 2019
Pittsburgh PA, USA

EURO 2019: 30th European Conference on Operational Research
June 23–26, 2019
Dublin, Ireland

5th Symposium on Quantitative Finance and Risk Analysis (QFRA 2019)
June 26–28, 2019
Kos Island, Greece